Description

In the context of artificial neural networks, the rectifier is an activation function defined as: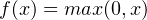

where x is the input to a Artificial Neuron.

from matplotlib import pyplot as plt
import numpy as np

def relu_forward(x):
    return x * (x > 0)


x = np.random.rand(10) - 0.5
x = np.append(x, 0.0)
x = np.sort(x)
y = relu_forward(x)

plt.style.use('fivethirtyeight')
fig, ax = plt.subplots()
ax.plot(x, y)
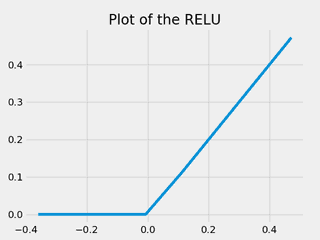
ax.set_title("Plot of the RELU")
plt.show()      
      

RELU derivative with respect to x defined as:

RELU used in computer vision and speech recognition using deep neural nets.

TensorFlow form of RELU:

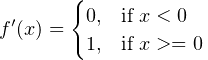
tf.nn.relu(features, name=None)

Pytorch form of RELU:

class torch.nn.ReLU(inplace=False)

Forward propagation EXAMPLE

/* ANSI C89, C99, C11 compliance                                      */
/* The following example shows the usage of RELU forward propagation. */
#include <stdio.h>

float relu_forward(float x){
   return x * (x > 0);
}

int main()  {
   float r_x, r_y;


   r_x = 0.1f;
   r_y = relu_forward(r_x);
   printf("RELU forward propagation for value x: %f\n", r_y);
   return 0;
}

Backward propagation EXAMPLE

/* ANSI C89, C99, C11 compliance                                       */
/* The following example shows the usage of RELU backward propagation. */
#include <stdio.h>

float relu_backward(float x){
   return (float)(x > 0.0);
}

int main()  {
   float r_x, r_y;


   r_x = 0.1f;
   r_y = relu_backward(r_x);
   printf("RELU backward propagation for value x: %f\n", r_y);
   return 0;
}