Description

Non-maximum suppression (NMS) is a post-processing step in many computer vision applications. In the context of object detection, it is used to discard redundant detections and to achieve a single bounding-box for each detected object. After applying the object detection method, the output looks like: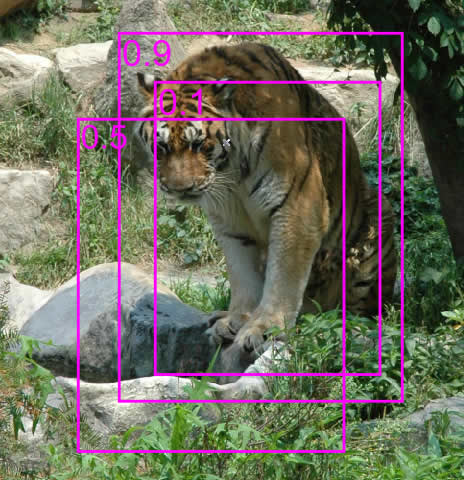

We can reduce the number of the boxes by non-maximum suppression or NMS by using Jaccard similarity of at least 0.5. After applying non-maximum suppression we will have:

Method

0. Sort all objects by score in descending order.
1. Compute area for every object.
2. Discard objects with score <= 0.6 (0.6 value as example)
3. Compute the intersection between 2 objects. A dominant object must have a highest score.
4. Compute the IOU or Jaccard index.
5. Discard non dominant object with IOU >= 0.5 (0.5 value as example).

EXAMPLE

/* ANSI C89, C99, C11 compliance                               	     */
/* The following example shows the usage of non-maximum suppression. */
#include <stdio.h>
#include <string.h>

#define MIN(a,b) (((a)<(b))?(a):(b))
#define MAX(a,b) (((a)>(b))?(a):(b))

#define DISCARD_BOXES_SCORE 0.6     /* boxes with score <= 0.6 to discard  */
#define DISCARD_BOXES_IOU   0.5     /* boxes with IOU >= 0.5 to discard    */
/*
   a---
   |  |
   ---b
*/
struct OBJ_DET {
   unsigned int n_class;      /* class of object                                 */
   float        r_score;      /* detection score                                 */
   unsigned int n_x_a;        /* bounding box upper left corner x coordinate     */
   unsigned int n_y_a;        /* bounding box upper left corner y coordinate     */
   unsigned int n_x_b;        /* bounding box bottom right corner x coordinate   */
   unsigned int n_y_b;        /* bounding box bottom right corner y coordinate   */
   unsigned int n_width;      /* bounding box width                              */
   unsigned int n_height;     /* bounding box height                             */
   unsigned int n_area;       /* bounding box area                               */
   unsigned int n_state;      /* state of detection: 0 - non  active, 1 - active */
};

/* insertion sort in descending order */
void insertion_sort_do(struct OBJ_DET *p_st, size_t n_size) {
   size_t         i, j;
   struct OBJ_DET st_val;


   for (i = 1; i < n_size; i++) {
      memcpy(&st_val, &p_st[i], sizeof(struct OBJ_DET));
      for (j = i; j > 0 && st_val.r_score > p_st[j - 1].r_score; j--) {
         memcpy(&p_st[j], &p_st[j - 1], sizeof(struct OBJ_DET));
      }
      memcpy(&p_st[j], &st_val, sizeof(struct OBJ_DET));
   }
}

/* The Jaccard index, also known as Intersection over Union (IoU) and the Jaccard similarity coefficient. */
float intersection_over_union(unsigned int n_area_inter, unsigned int n_area_a, unsigned int n_area_b)   {
   return (float)n_area_inter / (float)(n_area_a + n_area_b - n_area_inter);
}


int main() {
   struct OBJ_DET st_ds[3] = {{0, 0.7f, 1, 1, 0, 0, 4, 4, 0, 1}, {0, 0.2f, 2, 2, 0, 0, 4, 4, 0, 1}, {0, 0.8f, 1, 1, 0, 0, 4, 4, 0, 1}};
   size_t         i, j, n_size;
   int            z_xx_a, z_yy_a, z_xx_b, z_yy_b, z_w, z_h;
   float          r_iou;


   
   n_size = 3;                                                 /* number of objects  */
   insertion_sort_do(&st_ds[0], n_size);                       /* sort detections in descending order */
   for (i = 0; i < n_size; i++)  {                             /* calculate area */
      st_ds[i].n_area = st_ds[i].n_width * st_ds[i].n_height;
      st_ds[i].n_x_b = st_ds[i].n_x_a + st_ds[i].n_width;
      st_ds[i].n_y_b = st_ds[i].n_y_a + st_ds[i].n_height;
      if (st_ds[i].r_score <= DISCARD_BOXES_SCORE)             /* discard object */
         st_ds[i].n_state = 0;
   }
   for (i = 0; i < n_size; i++)  {
      if (st_ds[i].n_state != 0) {
         for (j = 0; j < n_size; j++)  {
            if ((i != j) && (st_ds[j].n_state != 0) && (st_ds[i].n_class == st_ds[j].n_class)) {
               z_xx_a = MAX(st_ds[i].n_x_a, st_ds[j].n_x_a);
               z_yy_a = MAX(st_ds[i].n_y_a, st_ds[j].n_y_a);
               z_xx_b = MIN(st_ds[i].n_x_b, st_ds[j].n_x_b);
               z_yy_b = MIN(st_ds[i].n_y_b, st_ds[j].n_y_b);               
               z_w = z_xx_b - z_xx_a;
               z_h = z_yy_b - z_yy_a;
               if ((z_w > 0) && (z_h > 0))   {
                  r_iou = intersection_over_union(z_w * z_h, st_ds[i].n_area, st_ds[j].n_area);
                  if (r_iou >= DISCARD_BOXES_IOU)
                     st_ds[j].n_state = 0;                     /* discard object */
               }
            }
         }
      }
   }
   for (i = 0; i < n_size; i++)  {
      if (st_ds[i].n_state != 0)
         printf("Object %lu is active\n", i);
   }
   return 0;
}